Consider Sounds Created by a Flute Continuously

Flute acoustics: an introduction to how a flute works
How does a flute work? This introduction gives first the simple explanations, then the subtleties. It requires no mathematics, nor any special acoustics knowledge. Some more technical references are listed near the end of this page. (There is also a database of flute fingerings.)Overview
The flutist blows a rapid jet of air across the embouchure hole. The pressure* inside the player's mouth is above atmospheric (typically a few tens of kPa: enough to support a few tens of cm height difference in a water manometer). The work done to accelerate the air in this jet is the source of power input to the instrument. The player provides power continuously: in a useful analogy with electricity, it is like DC electrical power. Sound, however, requires an oscillating motion or air flow (like AC electricity). In the flute, the air jet, in cooperation with the resonances in the air in the instrument, produces an oscillating component of the flow. Once the air in the flute is vibrating, some of the energy is radiated as sound out of the end and any open holes. A much greater amount of energy is lost as a sort of friction (viscous loss) with the wall. In a sustained note, this energy is replaced by energy put in by the player. The column of air in the flute vibrates much more easily at some frequencies than at others (i.e. it resonates at certain frequencies). These resonances largely determine the playing frequency and thus the pitch, and the player in effect chooses the desired set of resonances by choosing a suitable combination of keys. In this essay, we look at these effects one by one.
(* We have a separate page on air speed, air flow, pressure and power in woodwind and brass instruments.)
The air jet vibrates
The jet of air from the player's lips travels across the embouchure-hole opening and strikes against the sharp further edge of the hole. If such a jet is disturbed, then a wave-like displacement travels along it and deflects it so that it may blow either into or out of the embouchure hole. The speed of this displacement wave on the jet is just about half the air-speed of the jet itself (which is typically in the range 20 to 60 metres per second, depending on the air pressure in the player's mouth). The origin of the disturbance of the jet is the sound vibration in the flute tube, which causes air to flow into and out of the embouchure hole. If the jet speed is carefully matched to the frequency of the note being played, then the jet will flow into and out of the embouchure hole at its further edge in just the right phase to reinforce the sound and cause the flute to produce a sustained note. To play a high note, the travel time of waves on the jet must be reduced to match the higher frequency, and this is done by increasing the blowing pressure (which increases the jet speed) and moving the lips forward to shorten the distance along the jet to the edge of the embouchure hole. These are the adjustments that you gradually learn to make automatically when playing the flute. Flutists are usually taught to reduce the lip aperture when playing high notes.The sketch at right represents a cross section of the flute at the embouchure, with the jet being deflected alternately up and down, out of and into the bore.
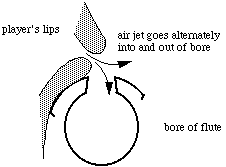
The flute is an open pipe
The flute is open at both ends. It's obvious that it's open at the far end. If you look closely at someone playing a flute, you'll see that, although player's lower lip covers part of the embouchure hole, s/he leaves a large part of the hole open to the atmosphere, as shown in the sketch above. Let's begin by considering a pipe that is simpler than a flute. First, we shall pretend that it is a simple cylindrical pipe---in other words we shall assume that all holes are closed (down to a certain point, at least), that the head is cylindrical, and we shall replace the side mounted embouchure hole with a hole at the end. In fact, this is more like a shakuhachi than a flute. It's a crude approximation, but it preserves much of the essential physics, and it's easier to discuss. (We shall introduce the effects of finger holes and the embouchure geometry below, or you can consult our research papers on this topic.)

The animation below is from Open vs closed pipes (Flutes vs clarinets), which gives a more detailed explanation. It shows a shows a pulse of high pressure reflecting in a pipe open to the air at both ends. Note that a complete cycle of vibration is the time taken for the pulse to travel twice the length L of the flute (once in each direction). The pulse travels at the speed of sound v, so the cycle would repeat at a frequency of v/2L, as we shall see again below.
The natural vibrations of the air in the flute are due to resonances. The reflecting pulse of air in the animation is an example of such a resonance, the fundamental or lowest resonance of the flute. There is more about resonances in the page on standing waves. What standing waves or resonances are possible in an open cylindrical tube? We shall now answer this question in terms of sine waves and harmonics.
The fact that the pipe is open to the air at the ends means that the total pressure at the ends must be approximately atmospheric pressure or, in other words, the acoustic pressure (the variation in pressure due to sound waves) is zero. These points are called pressure nodes, and they effectively lie past the end of the tube by a small distance (about 0.6 times the radius, as shown: this distance is called the end correction). Inside the tube, the pressure need not be atmospheric, and indeed for the first resonance, the maximum variation in pressure (the pressure anti-node) occurs at the middle. The standing wave is sketched below. The bold line is the variation in pressure, and the fine line represents the variation in the displacement of the air molecules. The latter curve has anti-nodes at the ends: air molecules are free to move in and out at the open ends. (Note that a node for pressure and a node for air motion are not the same thing: indeed, pressure nodes often coincide with motion anti-nodes and vice versa. See pipes and resonances. The difference between closed and open pipes is explained in Open vs closed pipes (Flutes vs clarinets), which compares them using wave diagrams, air motion animations and frequency analysis, or some more flow animations.)
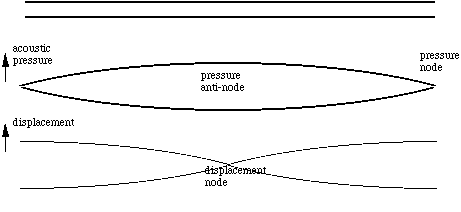
The wave shown above is the longest standing wave that can satisfy this condition of zero pressure at either end. In the figure below, we see that it has a wavelength twice as long as the flute. The frequency f equals the wave speed v divided by the wavelength l, so this longest wave corresponds to the lowest note on the instrument: C4 on a C foot instrument. (Flutists please note: this page uses the standard note names, not the names sometimes used by flutists.) You might want to measure the length L of your flute, take the speed of sound as v = 350 metres per second for sound in warm, moist air, and calculate the expected frequency. Then check the answer in the note table. (You will find that the answer is only approximate, because of end corrections.)
You can play C4 on the flute with this fingering, but you can also play other notes by blowing harder, or by narrowing the lip aperture (either gives a faster jet). These other notes correspond to the shorter wavelength standing waves that are possible, subject to the condition that the sound pressure be zero at both ends. The first several of these are shown in the diagram below.
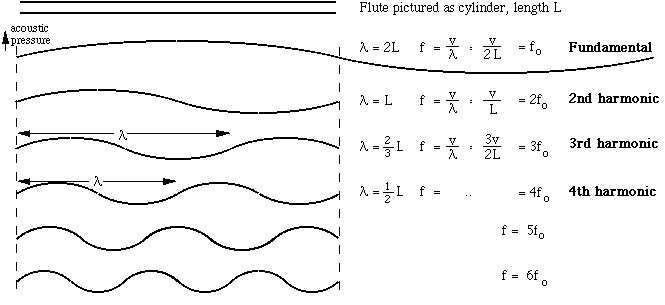
The series of notes with frequency fo, 2fo, 3fo etc is called the harmonic series, and notes with these frequencies have the pitches shown below. With all the tone holes closed, the first ten or so resonances of the flute are approximately in this ratio, so you can play the first seven or eight of the series by closing all the tone holes and blowing successively harder (or by narrowing the lip aperture). Note the half sharp on the seventh harmonic - it falls roughly midway between A6 and A#6. (You might be interested to compare this with the analogous diagram and sound files for the clarinet, which has only the odd harmonics present. There is also a more detailed discussion of the harmonic series of open and closed pipes. Also see a warning about the words 'fundamental' and 'harmonic'.)
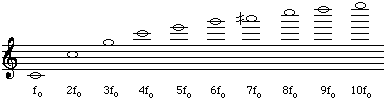
Each of the standing waves in the sketch above corresponds to a sine wave. The sound of the flute is a little like a sine wave (a very pure vibration) when played softly, but successively less like it as it is played louder. To make a repeated or periodic wave that is not a simple sine wave, one can add sine waves from the harmonic series. So C4 on the flute contains some vibration at C4 (let's call its frequency fo), some at C5 (2fo), some at G5 (3fo), some at C6 (4fo), etc. The 'recipe' of the sound in terms of its component frequencies is called its spectrum. (See sound spectrum for an explanation.) Looking at real sound spectra for played C4 (Open a new window for C4) you will see that, at pianissimo, the first harmonic (fundamental) and the frequency of the note C4 dominates, and that the higher harmonics become more important as the note is played more loudly, and as the flute develops a richer tone and sounds less and less like a sine wave. (For a detailed explanation, see Loudness and timbre.)
How the air jet and pipe work together
To sum up the preceding sections: the bore of the flute has several resonances, which are approximately in the ratios of the harmonics, 1:2:3:4 etc, but successively more approximate with increasing frequency--we'll see why below under frequency response. The air jet has its own natural frequency that depends on the speed and length of the jet. To oversimplify somewhat, the flute normally plays at the strongest bore resonance that is near the natural frequency of the jet. (We shall see below how register holes are used to weaken the lower resonance or resonances and thus make one of the higher resonances the strongest.)When the flute is playing, the jet is oscillating at one particular frequency. But, especially if the vibration is large, as it is when playing loudly, it generates harmonics (see What is a sound spectrum?). For low notes, the first several harmonics are supported by standing waves. However for high notes, the resonances of the flute are no longer harmonic, so only a small number of harmonics---only one in the third and fourth octave are supported by resonances of the bore. Played loudly however, harmonics of the vibration are present in the spectra, as you can see by looking at the spectra for any note.
Opening tone holes
If you open the tone holes, starting from the far end, you make the pressure node move closer up the pipe - it's rather like making the pipe shorter. On the Boehm flute, each opened tone hole raises the pitch by a semitone. After you open 4 holes on a C foot flute, as shown below, you have the fingering for E4, which is shown below. (Open a new window for E4).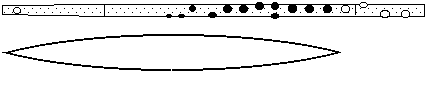
For the moment, we can say an open tone hole is almost like a 'short circuit' to the outside air, so the first open tone hole acts approximately as though the flute were 'sawn off' near the location of the tone hole. We shall return to qualify these assumptions below when we discuss register holes and cross fingerings. (For the technically minded, we could continue the electrical analogy by saying that the open tone hole is actually more like a low value inductance, and so it behaves more like a short circuit at low frequencies than at high. We return to this point when discussing cut-off frequencies below.)
Register holes
Holes can also serve as register holes. For instance, if you play C4 and then lift your left thumb, you are opening a hole halfway down the instrument. This makes the fundamental and the odd harmonics impossible, but hardly affects the even harmonics, which have a node there. So the flute 'jumps up' to C5 (2f1), and will also play C6, G6 etc. Here the register hole makes the played note (at least) one octave higher, because it is halfway along the working length of the flute and so permits the second harmonic of the fundamental C4. The example shown is not a standard fingering, but a register hole at half the length is used for the standard fingerings for D5 and others.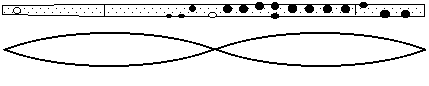
When the desired wavelength is short (i.e. for high notes) one can open a register hole at a different fraction of the length. For example, the fingering for D6 uses a register hole at approximately one third of the working length for G4, and so facilitates the third harmonic of G4 (and thus produces a note a twelfth higher than G4). The fingering for G6 also uses the working length for G4, but has a register hole about one quarter of the way along, and so facilitates the fourth harmonic.


One of the alternative fingerings for D#6 uses the working length for D#4 but has two register holes, at one quarter and one half the wavelength. Notes in the third octaves of all flutes rely heavily on using tone holes as register holes. Specific examples are explained on the pages for these notes. (See Flute Acoustics and choose a note above D#6.)
Acoustic impedance of the flute
The way in which the jet flows into and out of the flute depends upon the acoustic impedance at the embouchure hole, which is why we measure this quantity. The acoustic impedance is the ratio of the sound pressure to the oscillating air flow. (See Acoustic impedance for more detail.) If the impedance is low, air flows in and out readily and a loud sound can be produced. In fact, the resonances, which are the frequencies for which the acoustic impedance is very small, are so important that they 'capture' the behaviour of the air jet, and so the flute will play only at a frequency very close to a resonance. We discuss the acoustic impedance below, under Frequency response of the flute. There is further explanation on What is acoustic impedance and why is it important? and also a discussion of the impedance for C4.Cross fingering
On the modern or Boehm flute, successive semitones are played by opening a tone hole dedicated to that purpose. There are twelve semitones in an octave, so that one needs to open twelve keys in a chromatic scale before going from say D4 in the first register to D5 in the second register. (Because of the use of register holes for D5 and D#5, the fingerings do not repeat exactly over an entire octave, but only between E4/5 and C#5/6.) Twelve holes exceeds the number of fingers on standard players, particularly when the right thumb is employed to support the instrument. Boehm's key system employs clutches so that one finger can close more than one hole.Flutes in the baroque and early classical periods had few keys. (See The anatomy and evolution of the flute.) They had six open holes covered by the three large fingers on each hand. Opening these holes in sequence gave the 'natural' scale of the instrument, which was D major. Writing X for closed hole and O for open, the fingering chart for such an instrument is approximately:
with E5 to B5 using the same fingerings as E4 to B5. (Much more detail on fingerings and how they work is given on the pages for baroque and classical flutes.)On such instruments, cross fingerings are used to produce some of the intervening notes. In a cross fingering, further holes are closed downstream from the first open hole. For example, the fingering for F4/5 on the baroque flute is:
- F4/5 : XXX XOX
The effect of cross fingerings is frequency dependent. The extent of the standing wave beyond an open hole increases with the frequency, especially for small holes. This has the effect of making the effective length of the flute increase with increasing frequency. As a result, the impedance minima at higher frequencies tend to become flatter than strict harmonic ratios. One effect of this is that some cross fingerings cannot be used in both first and second register: the cross fingering used for G# in the first register will be too flat in the second register, or may not even play a note near G# at all. (See for example the fingerings for G#4 and G#5 on the baroque flute.)
A further effect of the disturbed harmonic ratios of the minima in impedance is that the harmonics that sound when a low note is played will not 'receive much help' from resonances in the instrument. (Technically, the bore does not provide feedback for the jet at that frequency, and nor does it provide impedance matching, so less of the high harmonics are present in the jet and they are also less efficiently radiated as sound.) As a result, the sound spectra for notes such as F4 and G#4 on the baroque flute have weaker higher harmonics, and so these notes are less loud and have darker or more mellow timbre than do the notes on either side.We noted previously that the 'natural' scale of these instruments is D major: in D and in B minor they use no cross fingerings, so their timbre is bright. In Eb major or C minor, their timbre is dark and they play more quietly. These observations are also true of the baroque oboes, baroque (and modern) recorders, and approximately true of the baroque bassoon. I suspect that this has contributed to the different qualities associated with different keys: keys with a couple of sharps are associated with bright and relatively loud winds, whereas keys with a few flats are associated with dark and quiet winds. For more information on the acoustics of cross fingerings, download a scientific paper on the topic.
'Lipping' up and down
The design of a flute involves compromises and many notes require slight pitch adjustment by the player. (See Tuning woodwinds.) Players lower the pitch mainly by a combination of drawing the chin back or pushing it forward, rolling the flute's embouchure hole towards them or away and changing the jet geometry. These actions do several things: (i) they increase the fraction of the embouchure hole that is covered by the lower lip, thereby decreasing the size of the hole opening to the atmosphere, (ii) they decrease the solid angle available into which the sound wave can radiate (informally: they 'get in the way of' the radiation), and (iii) they decrease the length and change the angle of the jet .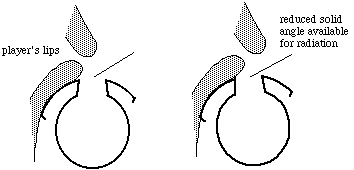
Effects (i) and (ii) increase the effective length of the flute and so make the resonant frequencies lower and the note flatter. Rolling the embouchure away and/or extending the lower jaw have the reverse effects, and so raise the pitch. Technically, these actions work because they change the radiation impedance at the embouchure: when a note is 'lipped down', the embouchure hole is "less open" (both the hole and angle are smaller so there is more impedance to radiation from the bore to the external field). The effects of the jet itself are more complicated.
We have measured these effects explicitly by installing our impedance measuring equipment in a flute head and measuring the impedance at the embouchure hole. (This is the impedance of the radiation field, 'looking out' from inside the blowhole, which is partially blocked by the lower lip. The flutist's lip and face also provide a baffle that reduces the angle for radiation. These results are reported in a recent conference paper - see our research papers site.) The interval that can be lipped depends on the details of the impedance spectrum and on some properties of the jet. It is easier to adjust the pitch of notes using a short length of tube, whose impedance spectra have fewer and shallower harmonic minima than do those of long tube fingerings. The analogous effects are much bigger on the shakuhachi, and are described on that site.
The cork and the 'upstream space'
Between the point where the embouchure riser meets the main bore of the flute and cork in the closed end of the instrument is a small volume of air. The cork is normally positioned to be about 17 mm from the centre of the embouchure hole (the exact value varies from player to player - see tuning wind instruments). Any very substantial variation seriously upsets the internal tuning of the flute. So how does this work?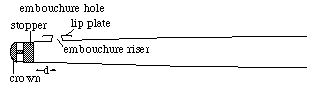
This 'upstream air' acts like a spring - when you compress it, the pressure rises. The air in the embouchure riser tube can be considered as a mass. Together they can resonate like a mass bouncing on a spring (ie they form a Helmholtz resonator).This has a resonance over a broad range of frequencies, but centred at about 5 kHz. At much lower frequencies, which is to say over the playing range of the flute, it acts as an impedance in parallel with the main part of the bore, but an impedance whose magnitude decreases with frequency. The primary effect of this is good: with the cork correctly placed, it compensates for the frequency dependent end effects at the other end of the flute and so keeps the registers in tune with each other. On the other hand, it does reduce the variation in impedance with frequency when the frequency approaches the Helmholtz resonance, and so is one of the effects that limits the upper range of the instrument. If you push the cork in, as Charanga style players do, you can go further up into the fourth octave, but at the expense of having an instrument whose octaves are badly out of tune. If you want to know more about this effect, download our technical paper about it. To scale the highest reaches of the flute's range, search for 'high playability' fingerings on the virtual flute and the report on F#7 and G7
The important message for flutists, however, is this. Among the orchestral winds, the flutes have the simplest method of adjusting their internal intonation. If your octaves are narrow, try pushing the cork in a little. If they are wide, pull it out. You will of course have to move the tuning slide as well. See also tuning wind instruments.
Cut-off frequencies
When we first discussed tone holes, we said that, because a tone hole opens the bore up to the outside air, it shortened the effective length of the tube. For low frequencies, this is true: the wave is reflected at or near this point because the hole provides a low impedance 'short circuit' to the outside air. For high frequencies, however, it is more complicated. The air in and near the tone hole has mass. For a sound wave to pass through the tone hole it has to accelerate this mass, and the required acceleration (all else equal) increases as the square of the frequency: for a high frequency wave there is little time in half a cycle to get it moving.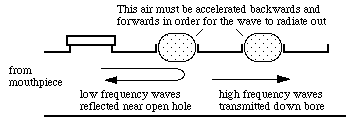
So high frequency waves are impeded by the air in the tone hole: it doesn't 'look so open' to them as it does to the waves of low frequency. Low frequency waves are reflected at the first open tone hole, higher frequency waves travel further (which can allow crossfingering) and sufficiently high frequency waves travel down the tube past the open holes. Thus an array of open tone holes acts as a high pass filter: some thing that lets high frequencies pass but rejects low frequencies. (See filter examples.)
The cut-off frequency for the Boehm flute is a little above 2 kHz. For example, in the acoustic response curve for A4, you will see that the first four or five resonances become gradually weaker with frequency--this is due to the increasing importance of energy losses due to the 'friction' (viscous loss) between the air and the wall. Above 2 kHz, however, the resonances are suddenly much weaker: waves with these frequency propagate down the bore and are radiated gradually from successive tone holes. The remaining weak standing waves produce resonances with a different frequency spacing, as we shall see in the next section. Before we move on, however, compare the A4 graph with that for B3. The latter is the lowest note on the flute, so there are no open tone holes and therefore no cut-off frequency. Consequently, the resonances fall gradually and uniformly with frequency over the whole range.
For the lowest note or two on the flute, there is no array of open holes and so there is no cutoff frequency due to that effect. In principle, if the higher harmonics were strong enough, one would expect this to lead to a different timbre of these notes. One way to avoid this--a way that is used for the oboe and clarinet--is to supply a bell that radiates high frequencies but not low, and which has a cut-off frequency comparable with that of the tone hole array. The flute has less radiated power at high frequencies than do the oboe and clarinet, so the need for a bell to 'homogenise' the timbre is rather less. However, a bell would increase high frequency radiation, both for long and short tube notes, and the pinschofon is the name of such an instrument.
(This technical paper gives measurements and analyses of cutoff frequencies and crossfingering in baroque, classical and modern flutes. There is also a more detailed explanation of cut-off frequencies and their effects here.)
Frequency response of the flute
So now let's look at the acoustic impedance spectrum of the modern flute. We'll choose the fingering used for C#5 and C#6, with nearly all tone holes open. It is shown in the graph below. (This graph covers a wide frequency range, but does not show much fine detail. For more detail, see C#5.)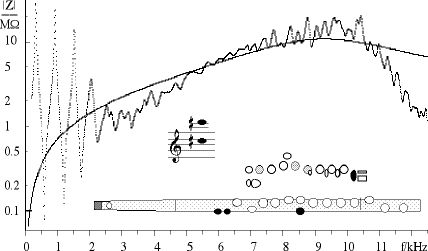
Below about 2.5 kHz, this curve looks like that for a simple cylindrical pipe with about half the length of the flute, because the tone holes are open in the bottom half of the instrument. The first three minima all support standing waves, and you can therefore play the notes C#5, C#6 and G#6 with this fingering. However, above 2.5 or 3 kHz, the resonances become much weaker. This is because of the high pass filter mentioned above under cut off frequencies. Higher still, around 5 kHz, the resonances almost disappear completely, because they are shorted out by the Helmholtz resonator discussed above under the cork and the 'upstream space'. Above this frequency range, the Helmholtz resonator is no longer a short circuit, so the resonances reappear, although they are weak because of the 'friction' of the air with the walls (increased effect of viscothermal losses at high frequencies).
Notice, however, an important difference. The spacing of peaks or troughs in the graph at the low frequency end is about 600 Hz (roughly the frequency of C#5, and corresponding to a standing wave in the half of the flute with no tone holes). At high frequencies, the spacing of peaks or troughs is about 260 Hz. This is the frequency of C4, and corresponds to the standing wave over the whole length of the flute. At these high frequencies, the wave in the bore of the flute propagates straight past the open tone holes, not 'noticing' that they are there, because of the inertia of the air discussed above under cut off frequencies. A human player cannot blow air fast enough to excite a fundamental frequency in this range. For a loud note in the normal range, some high harmonics will fall in this range. However, these harmonics have little need of the flute as a resonator, so the tuning of these ultra high resonances has little practical importance.
Finally, notice the general shape of the curve, which has a broad maximum at about 9 or 10 kHz. This is due to the relatively narrow embouchure riser: the tube of air linking the main bore to the lip plate. The air in this tube and a little bit outside at both ends (the end effects) is itself a resonant tube, whose resonance occurs over a broad range of frequencies because the tube's width is comparable with its length. The solid line on the graph is the theoretical impedance of a truncated cone having the geometry of the embouchure riser, including end effects. Some more detail is given in our technical paper about the end effects on the flute.
Other flutes: recorder, shakuhachi, dizi, pan pipes, ocarina and relatives
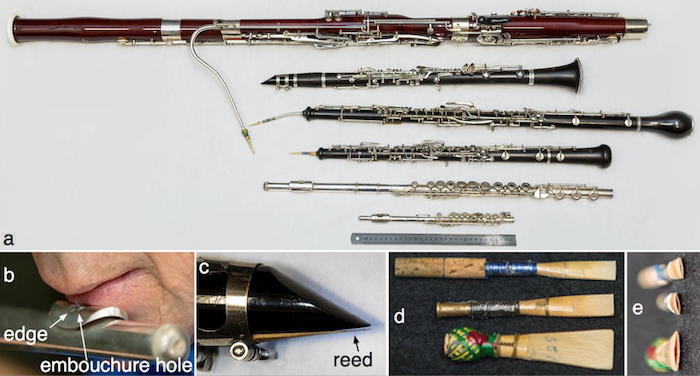
Flutes are a diverse family, whose earliest examples are 40,000 years old. Many cultures have developed flutes of different sorts. The photo below shows some of the sub-families.
(a) is the (alto) recorder, whose chief difference from transverse flutes is a windway. Here, the windway geometry forms the air jet, instead of leaving that to the player's lips. This makes the recorder a relatively easy instrument for beginners.
The shakuhachi (b) is a Japanese end-blown flute, whose end is sealed against the player's chin. This gives a more flexible air jet geometry, and thus more flexible pitch, but makes it a difficult instrument for beginners. The Chinese xiao (not shown) is another end-blown flute, though it has more tone holes. (See Shakuhachi acoustics)

The dizi (c) is a Chinese transverse flute, whose distinguishing feature is a thin membrane (indicated here by an arrow) stretched over a hole in the wall. The non-linearity of that membrane's pressure-volume curve has the effect of transferring power from low to high harmonics, giving it a brighter sound.
The panpipes or syrinx (d) are different in having a resonant duct for each note, each duct closed at the remote end.
The ocarina (e) uses a Helmholtz resonator to drive the jet, instead of a resonant duct. This allows it to play much lower notes than one would expect for its size: there is no simple relation between the wavelength and the length of the instrument. Here, the air inside acts as a spring, and the tiny masses of air in open tone holes act, in parallel, as vibrating masses on that spring: roughly speaking, a greater area of open tone holes gives a higher pitch. See Helmholtz resonator for explanation. Most ocarinas (e.g. the Chinese xun, not shown here) have fewer tone holes and consequently more complicated fingering—the nine tone holes on the model shown give it a fingering much like a simple transverse flute. On this flute, even the lowest notes use only one resonance, which gives the instrument its relatively soft, pure tone.
More detailed information
For more flute acoustics, return to the main flute site. Most of the individual note pages have descriptions of the acoustical effects relevant to their particular fingerings. If you are a flutist, you'll also want to check out the tools provided on the virtual flute.There is more detailed discussions of flute acoustics in several of our research papers that concern the acoustics of flutes and other instruments. The most recent paper concerns finger motion in flute playing.
Several flute questions are addressed on our FAQ in Music Acoustics. These include multiphonics, undertones, end effects and the importance of the material from which the flute is made.
For further reading, we propose
Also in this series:
Research and scholarship possibilities.
| |
A warning about the words 'fundamental' and 'harmonic'
These terms are often used inconsistently in music. Strictly, they refer to properties of periodic signals, like a musical note. However, musicians often use them to refer to notes played at different resonances.Sounds with definite pitch are usually periodic, meaning that they repeat after a period, called T. The fundamental frequency f (or sometimes f) is f = 1/T. The spectrum of a musical note usually* has several components or partials that fall at frequencies f, 2f, 3f, etc, called the first, second, third etc harmonic.
The resonances of an ideally thin, uniform string or air column have frequencies that fall in harmonic series. The resonances of real musical instrument strings or bores are not exactly harmonic. When a musician plays a note using one of the higher resonances, s/he often calls this �playing a harmonic�. example, a C flute, with all keys closed, has resonances very near C4 (f C4), C5 (2f C4), G5 (3f C4) etc. One can use this fingering to play notes near each of the first 7 or so resonances, as shown above. When the flutist uses this fingering to play G5, the fundamental of this note is 3f C4, and its second, third and fourth harmonics are at 6f C4, 9f C4 and 12f C4. Sometimes the flutist playing G5 with this fingering may say s/he is �playing the third harmonic�.
For most fingerings, however, the resonances are not in harmonic ratios. For example, the fingering ThOXX-OOO has resonances near C5 and D6 and will play either of these or a multiphonic combining the two.
* In untuned percussion, the partials are inharmonic (their frequencies are not in the ratio 1:2:3 etc). In tuned percussion and plucked strings, the frequency ratios are approximately in the ratio 1:2:3 etc, the difference usually being larger for higher frequencies.
This photo shows the common orchestral woodwinds in ascending order of pitch. Figure from The acoustics of woodwind musical instruments. Click to enlarge.)
williamswrecertrecan.blogspot.com
Source: https://newt.phys.unsw.edu.au/jw/fluteacoustics.html

0 Response to "Consider Sounds Created by a Flute Continuously"
Post a Comment